Exploring Decision Boundaries in Multi-Layer Perceptron (MLP)
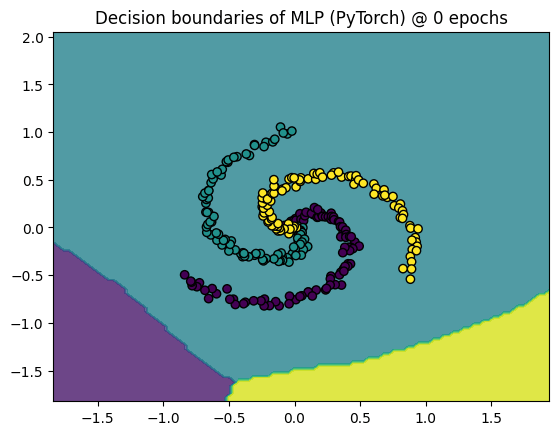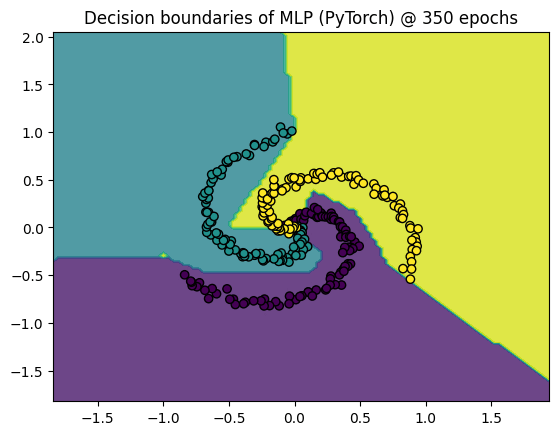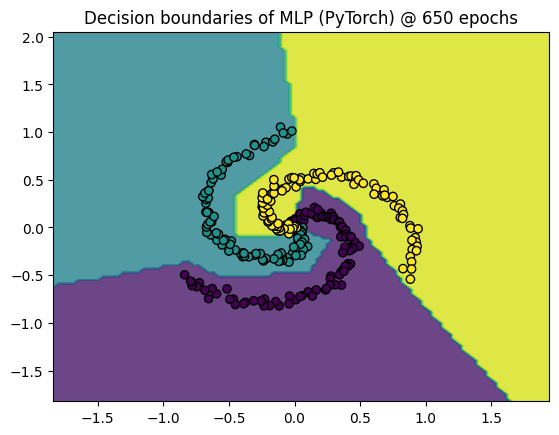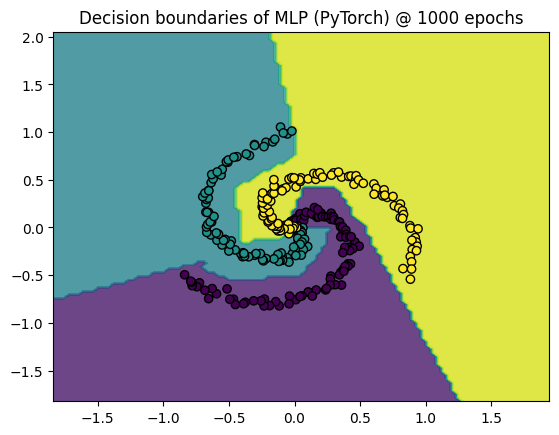
This tutorial is adopted from the NYU deep learning course NYU-DLSP20
Welcome to our very first tutorial on machine learning. In this post we will understand and produce the .gif we see above so let’s get started.
What is machine learning?
Before we get started, I would like to put you in the right frame of mind when thinking about what we hope to accomplish in this post. So the very first step is understanding machine learning. This is no tutorial on machine learning so we will avoid the details but the summary of it all is that we want to leverage data and build solutions with data instead of manually developing hand crafted solutions thereby making our new approach scalable. In essence, we can look at a problem in two ways, when given the input and output we figure out the transformation function that is universal (a hard problem) or we train (tune) a set of parameters in a certain architecture (the only little problem) with the input and output. The alternative is an easier approach and is much more scalable.
Now we have picked an easier step to solving a problem, we as scientist like to explain things so what exactly happens when we tune parameters with data. To demonstrate that, we will use a simple model architecture called multilayer perceptron and build our dataset.
The data samples used for this little demonstration is given as \(X_c(t) = t \left( \begin{matrix} \sin\left(\frac{2\pi}{C}(2t + c - 1)\right) + \mathcal{N}(0, \sigma^2) \\ \cos\left(\frac{2\pi}{C}(2t + c - 1)\right) + \mathcal{N}(0, \sigma^2) \end{matrix} \right)\quad 0\le t\le1,\quad c=1,\ldots,C\)
Where $C$ is the number of classes (in our case, 3), $\mathcal{N}$ is the normal distribution that adds some noise to samples, and the dimensions of the input and output data are given as $X_c\in\mathbb{R}^{m\times2}$ and $y\in\mathbb{R}^{m\times C}$ ($m$ is our number of training examples).
Our goal is to develop a multilayer perceptron which is a stack of logistic regression models (deep network) to solve the classification problem (one of 3 classes). We will build a network using Pytorch framework with one hidden layer of 10 hidden units.
For this exercise, we take the following steps
- Generate the synthetic data
- Define the model
- Train the model
- Make predictions
Generate the synthetic data
In this stage, we generate 100 samples for each class (so $m = 100$). The code snippet according to the equations above is as follows
# Generate synthetic data
t = torch.linspace(0, 1, 100).view(-1, 1)
X1 = t * torch.cat([torch.sin(2 / 3 * torch.pi * (2 * t)),
torch.cos(2 / 3 * torch.pi * (2 * t))], dim=1) + torch.randn(100, 2) * 0.03
X2 = t * torch.cat([torch.sin(2 / 3 * torch.pi * (2 * t + 1)),
torch.cos(2 / 3 * torch.pi * (2 * t + 1))], dim=1) + torch.randn(100, 2) * 0.03
X3 = t * torch.cat([torch.sin(2 / 3 * torch.pi * (2 * t + 2)),
torch.cos(2 / 3 * torch.pi * (2 * t + 2))], dim=1) + torch.randn(100, 2) * 0.03
X = torch.cat([X1, X2, X3], dim=0)
y = torch.cat([torch.zeros(100), torch.ones(100), 2 * torch.ones(100)]).long()
Define the model
Again we are developing a multilayer perceptron model with one hidden layer. The developed pytorch code snippet is as follows:
# Define the MLP model
class MLP(nn.Module):
def __init__(self):
super(MLP, self).__init__()
self.layers = nn.Sequential(
nn.Linear(2, 10),
nn.ReLU(),
nn.Linear(10, 10), # hidden layer
nn.ReLU(),
nn.Linear(10, 3),
nn.Softmax(dim=1)
)
def forward(self, x):
return self.layers(x)
At the output layer, we have 3 units for the 3 classes which is then squashed with the softmax function to produce probabilites that are compared with the labels of the classes (one-hot encoded labels)
Train the model and make predictions
We train the model with the adam optimizer and cross entropy loss. The code snippet for training the model is shown as follows:
# Initialize the model, loss function, and optimizer
model = MLP()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
# Train the model
for epoch in range(1001):
optimizer.zero_grad()
output = model(X)
loss = criterion(output, y_onehot)
loss.backward()
optimizer.step()
#####################
# ADD CODE TO MAKE PREDICTIONS AT DIFFERENT STAGES OF LEARNING
# AND PLOT THE DECISION BOUNDARIES
#####################
Obviously the code snippet does not contain the code to make predictions on test data to generate decision boundaries that can be visualized over the training stages. This is what we do next. The test data comprise a good distribution across the sample space of the training data which is then used to generate the boundary decisions of the model. The code snippet that implement that is as follows:
# Create a grid of points and predict
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
grid = torch.FloatTensor(np.c_[xx.ravel(), yy.ravel()])
# Train the model
for epoch in range(10001):
######################
# CODE TO TRAIN THE MODEL
######################
if epoch % 50 == 0:
with torch.no_grad():
predictions = model(grid)
_, predicted_classes = torch.max(predictions, 1)
Z = predicted_classes.reshape(xx.shape)
# Plot
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')
plt.title("Decision boundaries of MLP (PyTorch) @ " +
str(epoch) + " epochs")
plt.show()
The complete code is given below:
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
# Generate synthetic data
t = torch.linspace(0, 1, 100).view(-1, 1)
X1 = t * torch.cat([torch.sin(2 / 3 * torch.pi * (2 * t)),
torch.cos(2 / 3 * torch.pi * (2 * t))], dim=1) + torch.randn(100, 2) * 0.03
X2 = t * torch.cat([torch.sin(2 / 3 * torch.pi * (2 * t + 1)),
torch.cos(2 / 3 * torch.pi * (2 * t + 1))], dim=1) + torch.randn(100, 2) * 0.03
X3 = t * torch.cat([torch.sin(2 / 3 * torch.pi * (2 * t + 2)),
torch.cos(2 / 3 * torch.pi * (2 * t + 2))], dim=1) + torch.randn(100, 2) * 0.03
X = torch.cat([X1, X2, X3], dim=0)
y = torch.cat([torch.zeros(100), torch.ones(100), 2 * torch.ones(100)]).long()
# Plot the data
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')
# one hot encoding of labels
y_onehot = torch.zeros(y.shape[0], 3)
y_onehot[torch.arange(y.shape[0]), y] = 1
# Define the MLP model
class MLP(nn.Module):
def __init__(self):
super(MLP, self).__init__()
self.layers = nn.Sequential(
nn.Linear(2, 10),
nn.ReLU(),
nn.Linear(10, 10), # hidden layer
nn.ReLU(),
nn.Linear(10, 3),
nn.Softmax(dim=1)
)
def forward(self, x):
return self.layers(x)
# Initialize the model, loss function, and optimizer
model = MLP()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
# Create a grid of points and predict
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
grid = torch.FloatTensor(np.c_[xx.ravel(), yy.ravel()])
# Train the model
for epoch in range(1001):
optimizer.zero_grad()
output = model(X)
loss = criterion(output, y_onehot)
loss.backward()
optimizer.step()
if epoch % 50 == 0:
with torch.no_grad():
predictions = model(grid)
_, predicted_classes = torch.max(predictions, 1)
Z = predicted_classes.reshape(xx.shape)
# Plot
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')
plt.title("Decision boundaries of MLP (PyTorch) @ " +
str(epoch) + " epochs")
plt.show()
KUDOS for getting to the end of this post. Leave your comments and anything else 🙃.
P.S. It is all for learning and research purposes. Till next time. Au revoir 👋.
Enjoy Reading This Article?
Here are some more articles you might like to read next: